EJERCICIO RESUELTO DE MRUA. SOLUCION DEL EJERCICIO 3.46.

EJERCICIO 3.46.- Un camión viene disminuyendo su velocidad en forma uniforme, de 100 km/h a 50 km/h. Si para esto tuvo que frenar durante 1.500 m. Calcular:

  1. ¿Qué desaceleración produjeron los frenos?

  2. ¿Cuánto tiempo empleó para el frenado?. 

Se trata de un MRUA porque cambia la velocidad
a = constante

v = v0+ a . t

s = v0 .t+ 1/2 . a .t2

v2 = v0 2 + 2 . a . s

Los datos de ejercicio serían:
                     v0 = 100 km/h = 27,78 m/s
                     v = 50 km/h = 13,89 m/s 
                     s = 1500 m

Para calcular la aceleración utilizo:

v2 = v0 2 + 2 . a . s
(13,89 m/s)2 = (27,78 m/s) 2+ (2 . a .1500 m)
192,93 m2 /s2 = 771,73 m2 /s2  + ( a .3000 m)
192,93 m2 /s2 - 771,73 m2 /s2  = ( a .3000 m)
-578,8 m2 /s2  = ( a .3000 m)

-0,19 m /s2 = a
Para calcular el tiempo utilizo:

v = v0 + a . t
13,89 m/s = 27,78 m/s + ( (-0,19 m /s2) · t )
13,89 m/s - 27,78 m/s = ( (-0,19 m /s2) · t )
-13,89 m/s =  ( (-0,19 m /s2) · t )

 73,105 s = t

EJERCICIO DE MRU Y MRUA COMBINADO SOLUCIÓN DEL EJERCICIO 3.51)

EJERCICIO 3.51.- Un coche está parado en un semáforo, cuando este se pone en verde el conductor acelera hasta alcanzar 120 km/h, tardando para ello 1,25 minutos. A continuación y durante 6 minutos el coche circula a velocidad constante. Por último el conductor observa un semáforo en rojo a 90 m y se detiene delante de él. Resuelve:
  1. Tramo I.
  2. Tramo II
  3. Tramo III
  4. Distancia que en total recorre el coche y tiempo total transcurrido.
     
TRAMO I



TRAMO II


TRAMO III

Se trata de un MRUA porque cambia la velocidad
a = constante

v = v0+ a . t

s = v0 .t+ 1/2 . a .t2

v2 = v0 2 + 2 . a . s

Los datos de ejercicio serían:
                     v0 = 33,33 m/s (velocidad final del tramo anterior)
                     v = 0 m/s (porque se detiene)
                     s = 90 m

Para calcular la aceleración utilizo:

v2 = v0 2 + 2 . a . s
(0 m/s)2 = (33,33 m/s) 2+ (2 . a .90 m)
0 m2 /s2 = 1110,89 m2 /s2  + ( a .180 m)
0 m2 /s2 - 1110,89 m2 /s2  = ( a .180 m)
- 1110,89 m2 /s2  = ( a .180 m)

-6,17 m /s2 = a

Para calcular el tiempo utilizo:

v = v0 + a . t
0 m/s = 33,33 m/s + ( (-6,17 m /s2) · t )
0 m/s - 33,33 m/s = ( (-6,17 m /s2) · t )
- 33,33 m/s = ( (-6,17 m /s2) · t )

5,4 s = t
 

MRU Y MRUA COMBINADO (PROYECTO EL DESAFÍO)

Vamos ha estudiar uno de los pocos  casos de movimiento rectilíneo combinado de la vida real. Nos lo podemos encontrar en cualquier "parque de atracciones" como el de Isla Mágica en Sevilla. La atracción que vamos a analizar recibe el nombre de "El desafio".

Lo primero que vamos a hacer es intentar averiguar sus datos técnicos. Nosotros para realizar el estudio de uno de sus movimientos nos hemos quedado con estos.


No son los únicos por cierto ya que la atracción realiza numerosas variantes, pero vamos a  intentar resolver la más elemental de ellas, la que consiste en subir a velocidad constante y realizar una caida libre para frenar al final del trayecto.

Para ello pordemos distinguir 6 partes elementales del movimiento:

TRAMO 1 TRAMO 2 TRAMO 3 TRAMO 4 TRAMO 5 TRAMO 6
Arranque Subida Freno Espera Caida Parada final
MRUA
MRU
MRUA

MRUA
MRUA

Antes de empezar a observar los datos del ejercicio vamos a establecer las condiciones de contorno del mismo. Partimos del reposo el tramo 1 y nos paramos al final del tramo 3. Nos dejan caer en el tramo 5 y debemos deternos al final del tramo 6.

TRAMO 1 TRAMO 2 TRAMO 3 TRAMO 4 TRAMO 5 TRAMO 6
Arranque Subida Freno Espera Caida Parada final
MRUA
MRU
MRUA

MRUA
MRUA
a = a = a = a = 0 m/s2 a = a =
vo = 0 m/s

vo =

vo = 0 m/s vo =
v = v = v = 0 m/s v = 0 m/s v = v = 0 m/s
s = s = s = s = 0 m/s s = s =
t = t = t = t = t = t =

 Teniendo en cuenta que la altura de la torre es de 68 m y que durante 55 m estamos cayendo tenemos hasta 13 metros para detenernos.

TRAMO 1 TRAMO 2 TRAMO 3 TRAMO 4 TRAMO 5 TRAMO 6
Arranque Subida Freno Espera Caida Parada final
MRUA
MRU
MRUA

MRUA
MRUA
a = a = a = a = 0 m/s2 a = a =
vo = 0 m/s

vo =

vo = 0 m/s vo =
v = v = v = 0 m/s v = 0 m/s v = v = 0 m/s
s = s = s = s = 0 m/s s = 55 m s = 13 m
t = t = t = t = t = t =


Si tenemos en cuenta que la velocidad máxima se alcanzará al final de la caida (tramo 5) o bien la principio de la  frenada final (tramo 6). Transformamos los 51 km/h en 14,17 m/s para que esté expresado en las unidades del S.I.
 
TRAMO 1 TRAMO 2 TRAMO 3 TRAMO 4 TRAMO 5 TRAMO 6
Arranque Subida Freno Espera Caida Parada final
MRUA
MRU
MRUA

MRUA
MRUA
a = a = a = a = 0 m/s2 a = a =
vo = 0 m/s

vo =

vo = 0 m/s vo = 14,17 m/s
v = v = v = 0 m/s v = 0 m/s v = 14,17 m/s v = 0 m/s
s = s = s = s = 0 m/s s = 55 m s = 13 m
t = t = t = t = t = t =

Suponemos que la subida se realiza a velocidad constante y ulilizamos la velocidad máxima de subida en el tramo 2 (con lo cual tenemos información del final del primer tramo y del inicio del tramo 3)

TRAMO 1 TRAMO 2 TRAMO 3 TRAMO 4 TRAMO 5 TRAMO 6
Arranque Subida Freno Espera Caida Parada final
MRUA
MRU
MRUA

MRUA
MRUA
a = a = 0 m/s2 a = a = 0 m/s2 a = a =
vo = 0 m/s

vo = 5,8 m/s

vo = 0 m/s vo = 14,17 m/s
v = 5,8 m/s v = 5,8 m/s v = 0 m/s v = 0 m/s v = 14,17 m/s v = 0 m/s
s = s = s = s = 0 m/s s = 55 m s = 13 m
t = t = t = t = t = t =

Por últimos anotamos la aceleración de subida y la acelereción de frenada en los correspondientes tramo 1 y tramo 3 y ya tenemos anotados todos los datos técnicos que nos proporcionan :

TRAMO 1 TRAMO 2 TRAMO 3 TRAMO 4 TRAMO 5 TRAMO 6
Arranque Subida Freno Espera Caida Parada final
MRUA
MRU
MRUA

MRUA
MRUA
a = 1,5 m/s2 a = 0 m/s2 a = -2 m/s2 a = 0 m/s2 a = a =
vo = 0 m/s

vo = 5,8 m/s

vo = 0 m/s vo = 14,17 m/s
v = 5,8 m/s v = 5,8 m/s v = 0 m/s v = 0 m/s v = 14,17 m/s v = 0 m/s
s =  s = s = 8,41 m s = 0 m/s s = 55 m s = 13 m
t =  t = t = 2,9s t = t = t =


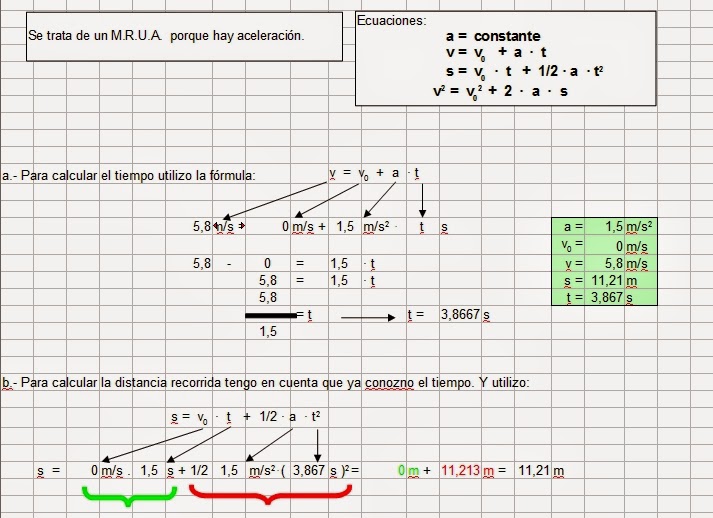
TRAMO 1: ARRANQUE

TRAMO 1TRAMO 2TRAMO 3TRAMO 4TRAMO 5 TRAMO 6
ArranqueSubidaFrenoEsperaCaidaParada final
MRUA
MRU
MRUA

MRUA
MRUA
a = 1,5 m/s2a = 0 m/s2a = -2 m/s2a = 0 m/s2a =a =
vo = 0 m/s

vo = 5,8 m/s

vo = 0 m/svo = 14,17 m/s
v = 5,8 m/sv = 5,8 m/sv = 0 m/sv = 0 m/sv = 14,17 m/sv = 0 m/s
s = 11,21ms =s =  s = 0 m/ss = 55 ms = 13 m
t = 3,87 st =t = t =t =t =


TRAMO 3: FRENADA

TRAMO 1TRAMO 2TRAMO 3TRAMO 4TRAMO 5 TRAMO 6
ArranqueSubidaFrenoEsperaCaidaParada final
MRUA
MRU
MRUA

MRUA
MRUA
a = 1,5 m/s2a = 0 m/s2a = -2 m/s2a = 0 m/s2a =a =
vo = 0 m/s

vo = 5,8 m/s

vo = 0 m/svo = 14,17 m/s
v = 5,8 m/sv = 5,8 m/sv = 0 m/sv = 0 m/sv = 14,17 m/sv = 0 m/s
s = 11,21ms =s = 8,41 ms = 0 m/ss = 55 ms = 13 m
t = 3,87 st =t = 2,9st =t =t =


 TRAMO 2: SUBIR 

Para poder resolver el tramo 2 ncesitamos más datos de los que tenemos en la tabla, pero voy a tener en cuenta que en el dibujo puedo deducir la distancia recorrida durante el tramo 2:


 
TRAMO 1TRAMO 2TRAMO 3TRAMO 4TRAMO 5 TRAMO 6
ArranqueSubidaFrenoEsperaCaidaParada final
MRUA
MRU
MRUA

MRUA
MRUA
a = 1,5 m/s2a = 0 m/s2a = -2 m/s2a = 0 m/s2a =a =
vo = 0 m/s

vo = 5,8 m/s

vo = 0 m/svo = 14,17 m/s
v = 5,8 m/sv = 5,8 m/sv = 0 m/sv = 0 m/sv = 14,17 m/sv = 0 m/s
s = 11,21ms = 48,38 ms = 8,41 ms = 0 m/ss = 55 ms = 13 m
t = 3,87 st =t = 2,9st =t =t =


TRAMO 1TRAMO 2TRAMO 3TRAMO 4TRAMO 5 TRAMO 6
ArranqueSubidaFrenoEsperaCaidaParada final
MRUA
MRU
MRUA

MRUA
MRUA
a = 1,5 m/s2a = 0 m/s2a = -2 m/s2a = 0 m/s2a = a =
vo = 0 m/s

vo = 5,8 m/s

vo = 0 m/svo = 14,17 m/s
v = 5,8 m/sv = 5,8 m/sv = 0 m/sv = 0 m/sv = 14,17 m/sv = 0 m/s
s = 11,21ms = 48,38 ms = 8,41 ms = 0 m/ss = 55 ms = 13 m
t = 3,87 st = 8,34 st = 2,9st =t = t =


TRAMO 5: CAÍDA 

TRAMO 1TRAMO 2TRAMO 3TRAMO 4TRAMO 5 TRAMO 6
ArranqueSubidaFrenoEsperaCaidaParada final
MRUA
MRU
MRUA

MRUA
MRUA
a = 1,5 m/s2a = 0 m/s2a = -2 m/s2a = 0 m/s2a = 1,825 m/s2a =
vo = 0 m/s

vo = 5,8 m/s

vo = 0 m/svo = 14,17 m/s
v = 5,8 m/sv = 5,8 m/sv = 0 m/sv = 0 m/sv = 14,17 m/sv = 0 m/s
s = 11,21ms = 48,38 ms = 8,41 ms = 0 m/ss = 55 ms = 13 m
t = 3,87 st = 8,34 st = 2,9st =t = 7,76 st =

TRAMO 6 : Parada final

TRAMO 1TRAMO 2TRAMO 3TRAMO 4TRAMO 5 TRAMO 6
ArranqueSubidaFrenoEsperaCaidaParada final
MRUA
MRU
MRUA

MRUA
MRUA
a = 1,5 m/s2a = 0 m/s2a = -2 m/s2a = 0 m/s2a = 1,825 m/s2a =-7,72 m/s2
vo = 0 m/s

vo = 5,8 m/s

vo = 0 m/svo = 14,17 m/s
v = 5,8 m/sv = 5,8 m/sv = 0 m/sv = 0 m/sv = 14,17 m/sv = 0 m/s
s = 11,21ms = 48,38 ms = 8,41 ms = 0 m/ss = 55 ms = 13 m
t = 3,87 st = 8,34 st = 2,9st =t = 7,76 st = 1,835 s

La única información que nos queda por saber es el tiempo de espera cuando estamos suspendidos en lo alto de la torre.

SOLUCIÓN DEL EJERCICIO 3.52


(EJERCICIO 3.52) Un coche lleva una velocidad de 120 km/h y en 15 s su velocidad se reduce hasta 75 km/h. A continuación circula 30 s a velocidad constante. Por último acelera durante 20 s hasta que su velocidad es de 100 km/h.

a.- Calcula o identifica todos los datos del tramo 1.
b.- Calcula o identifica todos los datos del tramo 2.
c.- Calcula o identifica todos los datos del tramo 3.
d.- Calcula la distancia que en total recorre el coche y el tiempo que emplea.





Ejercicio realizado por Victor Iglesias González E3A FISCA 2014/15

SOLUCIÓN A LOS EJERCICIOS DE MRUA PARA PRACTICAR





tiempo desplazamiento
Velocidad
inicial
Velocidad
final		 aceleración
1
10 s
200 m
0
40 m/s
 4 m/s2
2
1 minuto
875 m
0
105 km/h
 0.49 m/s2
3
30 s
1000 m
0
66.6 m/s
 2.22 m/s2
4
10 s
200 m
30 m/s
10 m/s
 2 m/s2
5
150 s
1875 m
90 km/h
0
 0.1 m/s2
6
50 s
300 m
72 km/h
-8 m/s
 -0.56m/s2
7
5.8 s
300 m
31.6
20 m/s
 -1 m/s2
8
4 s
80 m
40 m/s
0
 -10 m/s2
9
4 s
80 m
0
40 m/s
 +10 m/s2
10
50 s
1000 m
0
40 m/s
 0.8 m/s2
11
14.1 s
1000 m
0
141.4m/s
 10 m/s2
12
2 s
500 m
400 m/s
100 m/s
 150 m/s2




BIBLIOTECA DE IMÁGENES PARA SCRATCH: PERSONAS











BIBLIOTECA DE IMAGENES PARA SCRATCH: MICKEY MOUSE





EJERCICIOS DE MRUA PARA PRACTICAR

Completa el siguiente cuadro utilizando las unidades del S.I.


tiempo
 desplazamiento
Velocidad
inicial
Velocidad
final
 aceleración
1
10 s
?
0
?
 4 m/s2
2
1 minuto
?
0
105 km/h
?
3
30 s
1000 m
0
?
?
4
?
?
30 m/s
10 m/s
 -2 m/s2
5
150 s
?
90 km/h
0
?
6
50 s
300 m
72 km/h
?
?
7
?
300 m
?
20 m/s
 -1 m/s2
8
?
?
40 m/s
0
 -10 m/s2
9
4 s
?
0
40 m/s
?
10
?
1000 m
0
40 m/s
?
11
?
1000 m
0
?
 10 m/s2
12
?
500
400 m/s
100 m/s
?
Para comprobar las soluciones pincha aquí

BIBLIOTECA DE IMAGENES PARA SCRATCH: SIMPSON

























Suscribirse a: Entradas (Atom)